ML is becoming integrated into our lives, ranging from what we see on social media to making medical decisions. However, ML models are increasingly being executed behind closed APIs. There are good reasons for this: model weights may be unable to be revealed for privacy reasons if they are trained on user data (e.g., medical data) and companies want to protect trade secrets. For example, Twitter recently open-sourced their “For You” timeline ranking algorithm but couldn’t release the weights for privacy reasons. OpenAI has also not released weights for GPT-3 or 4.

As ML becomes integrated with our lives, there’s a growing need for assurances that the ML models have desirable properties and were executed honestly. For ML, we need assurances that the model ran as promised (computational integrity) and that the correct weights were used (while maintaining privacy). For example, for the GPT and Twitter ranking models, we would like to confirm that the model results are consistently unbiased and uncensored. How can we balance the need for privacy (of the user data and model weights) and transparency?

To accomplish this, we can use a cryptographic technique called ZK-SNARKs. ZK-SNARKs have seemingly magical properties of allowing a ML model owner to prove the model executed honestly without revealing the weights!

In the rest of the post, we’ll describe what ZK-SNARKs are and how to use them to balance the goals of privacy and transparency. We’ll also describe how to use our recently open-sourced framework zkml to generate ZK-SNARKs of ML models.

ZK-SNARKs for ML

It’s important to understand one of the key cryptographic building blocks that enable privacy-preserving computations: Zero-Knowledge Succinct Non-Interactive Argument of Knowledge (ZK-SNARK). ZK-SNARKs are a powerful cryptographic primitive that allows one party to prove the validity of a computation without revealing any information about the inputs to the computation itself! ZK-SNARKs also don’t require any interaction beyond the proof and don’t require the verifier of the computation to execute the computation itself.

ZK-SNARKs are also succinct, meaning they are small (typically constant or logarithmic size) relative to the computation! Concretely, for even large models, the proofs are typically less than 5kb. This is desirable since many kinds of cryptographic protocols require gigabytes or more of communication, saving up to up to six orders of magnitude of communication.

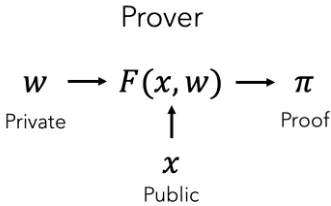
Given a set of public inputs (x) and private inputs (w), ZK-SNARKS can prove that a relation F(x,w) holds between the values without revealing the private inputs. For example, a prover can prove they know the solution to a sudoku problem. Here, the public inputs are the starting squares and the private inputs are the remainder of the squares that constitute the solution.

In the context of ML, ZK-SNARKs can prove that the ML model executed correctly without revealing the model weights. In this case, the model weights w are the private input, the model input features F and output O are part of the public input. In order to identify the model, we also include a model commitment C in the public input. The model commitment functions like a hash, so that with high probability if the weights were modified the commitments would differ as well. Thus x = (C,F,O). Then the relation we want to prove is that, for some private weight value w, having commitment C, the model outputs O on inputs F.

If a verifier is then given the proof π (and x), they can verify that the ML model ran correctly:

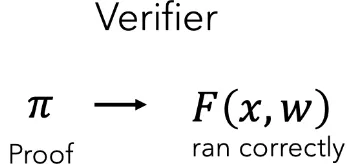
To give a concrete example, Twitter can prove they ran their ranking algorithm honestly to generate your timeline. A medical ML provider can also provide a proof that a specific regulator-approved model was executed honestly as well.

Using zkml for trustless execution of ML models

We’ve open-sourced our library zkml to construct proofs of ML model execution and allow anyone to verify these proofs. But first, let’s look at what a standard ML provider would do:

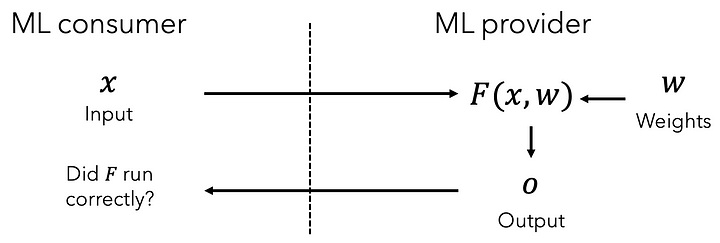
As we can see here, the ML consumer provides the inputs but has no assurances that the model executed correctly! With zkml, we can add a single step to provide guarantees that the model executed correctly! As we can see, the ML consumer doesn’t learn anything about the weights:

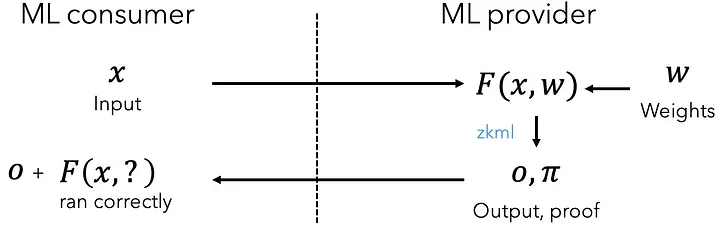
To demonstrate how to use zkml to trustlessly execute an ML model, we’ll construct a proof of a model that achieves 99.5% accuracy on MNIST, a standard ML image recognition dataset. zkml will generate the proof, but also the proving key and verification key which allows the prover to produce the proof (proving key) and the verifier to verify that the execution happened honestly (verification key). First, to construct the proof, proving key, and verification key, simply execute the following commands:

# Installs rust, skip if you already have rust installed  
curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh  
  
git clone https://github.com/ddkang/zkml.git  
cd zkml  
rustup override set nightly  
cargo build --release  
mkdir params_kzg  
  
# This should take ~8s to run the first time and ~4s to run the second time  
./target/release/time_circuit examples/mnist/model.msgpack examples/mnist/inp.msgpack kzg

This will construct the proof, where the proving key is generated during the process. Here, model.msgpack is the model weights and inp.msgpack is the input to the model (in this case, it’s an image of a handwritten 5). The proof generation will also generate the public values x (including the model commitment), which we’ll use in the next step. It will also generate a verification key, as we described above. You’ll see the following output:

<snip>  
final out[0] x: -5312 (-10.375)  
final out[1] x: -8056 (-15.734375)  
final out[2] x: -8186 (-15.98828125)  
final out[3] x: -1669 (-3.259765625)  
final out[4] x: -4260 (-8.3203125)  
final out[5] x: 6614 (12.91796875)  
final out[6] x: -5131 (-10.021484375)  
final out[7] x: -6862 (-13.40234375)  
final out[8] x: -3047 (-5.951171875)  
final out[9] x: -805 (-1.572265625)  
<snip>

The outputs you see here are the logits of the model, which can be converted to probabilities. As we can see, the 5th output is the largest, meaning the model correctly classified the 5.

Given the proof, a verifier can verify the ML model executed correctly without the model weights. Here, the vkey is the verification key, the proof is π, and the public_vals is the public output:

$ ./target/release/verify_circuit examples/mnist/config.msgpack vkey proof public_vals kzg  
  
Proof verified!

Which should show you that the proof verified correctly. Notice the verifier only needs the configuration, verification key, proof, and public values!

Stay tuned!

We’ll have more posts upcoming to describe the applications of zkml in more detail! Check out our open-source repository and if you’d like to discuss your idea or brainstorm with us, fill out this form!

Thanks to Yi Sun for comments on this blog post.